文章目录
-
- 逻辑函数的最简形式
- 逻辑函数的代数化简法
-
-
- 并项法
- 吸收法
- 消去法
- 配项法
- 示例1
- 示例2
-
逻辑函数的最简形式
1.化简逻辑函数的意义
L = A B + A ˉ B + A ˉ B ˉ = ( A + A ˉ ) B + A ˉ B ˉ = 1 ⋅ B + A ˉ B ˉ = B + A ˉ begin{aligned} L & =A B+bar{A} B+bar{A} bar{B} & =(A+bar{A}) B+bar{A} bar{B} & =1 cdot B+bar{A} bar{B} & =B+bar{A} end{aligned} L=AB+AˉB+AˉBˉ=(A+Aˉ)B+AˉBˉ=1⋅B+AˉBˉ=B+Aˉ

两个电路的逻辑功能完全相同。但简化电路使用的逻辑门较少,体积小且成本低。
化简的意义:根据化简后的表达式构成的逻辑电路简单,可节省器件,降低成本,提高工作的可靠性。
2.逻辑函数的常见表达形式
L = A C + C ˉ D A C ‾ ‾ ⋅ C ˉ ‾ D “与-或” 表达式 “与非-与非” 表达式 = ( A + C ˉ ) ( C + D ) “或-与” 表达式 = ( A + C ˉ ) ‾ + ( C + D ) ‾ ‾ “或非-或非” 表达式 = A ˉ C + C ˉ D ˉ ‾ “与-或-非” 表达式 begin{array}{rlrl} L & =frac{A C+bar{C} D}{overline{overline{A C}} cdot overline{bar{C}} D} & & text { “与-或” 表达式 } & & text { “与非-与非” 表达式 } & =(A+bar{C})(C+D) & & text { “或-与” 表达式 } & =overline{overline{(A+bar{C})}+overline{(C+D)}} & & text { “或非-或非” 表达式 } & =overline{bar{A} C+bar{C} bar{D}} & & text { “与-或-非” 表达式 } end{array} L=AC⋅CˉDAC+CˉD=(A+Cˉ)(C+D)=(A+Cˉ)+(C+D)=AˉC+CˉDˉ “与非–与非” 表达式 “与–或” 表达式 “或–与” 表达式 “或非–或非” 表达式 “与–或–非” 表达式
“与-或”表达式:也称为 “积之和 (Sum of Products,SOP)”表达式;
“或-与”表达式:也称为 “和之积(Products of Sum, POS)”表达式。
简化标准(最简的与-或表达式)
乘积项的个数最少(与门的个数少);
每个乘积项中包含的变量数最少(与门的输入端个数少)。
化简的主要方法:
1.公式法(代数法)
运用逻辑代数的基本定律和恒等式进行化简的方法。
2.图解法(卡诺图法)
逻辑变量的个数受限。
逻辑函数的代数化简法
方法:
并项法
A + A ˉ = 1 A+bar{A}=1 A+Aˉ=1
- L = A ˉ B ˉ C + A ˉ B ˉ C ˉ = A ˉ B ˉ ( C + C ˉ ) = A ˉ B ˉ L=bar{A} bar{B} C+bar{A} bar{B} bar{C}=bar{A} bar{B}(C+bar{C})=bar{A} bar{B} L=AˉBˉC+AˉBˉCˉ=AˉBˉ(C+Cˉ)=AˉBˉ
吸收法
A + A B = A A+A B=A A+AB=A
- L = A ˉ B + A ˉ B C D ( E + F ) = A ˉ B L=bar{A} B+bar{A} B C D(E+F)=bar{A} B L=AˉB+AˉBCD(E+F)=AˉB
消去法
$A+bar{A} B=A+B $
- L = A B + A ˉ C ‾ + B ˉ C ‾ = A B + ( A ˉ + B ˉ ) C = A B + A B C ‾ = A B + C begin{aligned} L & =A B+underline{bar{A} C}+underline{bar{B} C}=A B+(bar{A}+bar{B}) C & =A B+overline{A B C}=A B+C end{aligned} L=AB+AˉC+BˉC=AB+(Aˉ+Bˉ)C=AB+ABC=AB+C
配项法
A + A ˉ = 1 A+bar{A}=1 A+Aˉ=1
- L = A B + A ˉ C ˉ + B C ˉ ‾ = A B + A ˉ C ˉ + ( A + A ˉ ) B C ˉ = A B ‾ + A ˉ C ˉ ‾ + A B C ˉ ‾ + A ˉ B C ˉ ‾ = ( A B + A B C ˉ ) + ( A ˉ C ˉ + A ˉ C ˉ B ) = A B + A ˉ C ˉ begin{aligned} L & =A B+bar{A} bar{C}+underline{B bar{C}}=A B+bar{A} bar{C}+(A+bar{A}) B bar{C} & =underline{A B}+underline{bar{A} bar{C}}+underline{A B bar{C}}+underline{bar{A} B bar{C}} & =(A B+A B bar{C})+(bar{A} bar{C}+bar{A} bar{C} B) & =A B+bar{A} bar{C} end{aligned} L=AB+AˉCˉ+BCˉ=AB+AˉCˉ+(A+Aˉ)BCˉ=AB+AˉCˉ+ABCˉ+AˉBCˉ=(AB+ABCˉ)+(AˉCˉ+AˉCˉB)=AB+AˉCˉ
示例1
已知逻辑函数表达式为 L = A ˉ B D ˉ + A B ˉ D ˉ + A ˉ B D + A B ˉ C ˉ D + A B ˉ C D L=bar{A} B bar{D}+A bar{B} bar{D}+bar{A} B D+A bar{B} bar{C} D+A bar{B} C D L=AˉBDˉ+ABˉDˉ+AˉBD+ABˉCˉD+ABˉCD
要求:(1)最简的与-或逻辑函数表达式,并画出逻辑图;
(2)仅用与非门画出最简表达式的逻辑图。
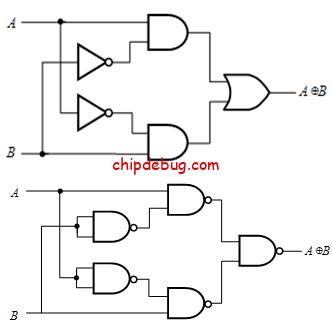
L = A ˉ B ( D ˉ + D ) + A B ˉ D ˉ + A B ˉ ( C ˉ + C ) D = A ˉ B + A B ˉ D ˉ + A B ˉ D = A ˉ B + A B ˉ ( D + D ˉ ) = A ˉ B + A B ˉ (与-或表达式) = A ˉ ‾ B + A B ˉ ‾ = A ˉ ‾ B ⋅ A B ˉ ‾ ‾ (与非-与非表达式) begin{aligned} L & =bar{A} B(bar{D}+D)+A bar{B} bar{D}+A bar{B}(bar{C}+C) D & =bar{A} B+A bar{B} bar{D}+A bar{B} D & =bar{A} B+A bar{B}(D+bar{D}) & =bar{A} B+A bar{B} text { (与-或表达式) } & =overline{overline{bar{A}} B+A bar{B}} & =overline{overline{bar{A}} B cdot overline{A bar{B}}} text { (与非-与非表达式) } end{aligned} L=AˉB(Dˉ+D)+ABˉDˉ+ABˉ(Cˉ+C)D=AˉB+ABˉDˉ+ABˉD=AˉB+ABˉ(D+Dˉ)=AˉB+ABˉ (与–或表达式) =AˉB+ABˉ=AˉB⋅ABˉ (与非–与非表达式)
示例2
试对逻辑函数表达式 L = A ˉ B ˉ C + A B ˉ C ˉ L=bar{A} bar{B} C+A bar{B} bar{C} L=AˉBˉC+ABˉCˉ 进行变换,仅用或非门画出该表达式的逻辑图。
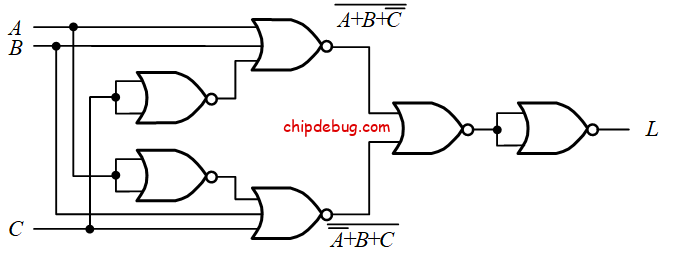
L = A ˉ B ˉ C + A B ˉ C ˉ = A ˉ B ˉ C ‾ ‾ + A B ˉ C ˉ ‾ ‾ = A + B + C ˉ + A ˉ + B + C ‾ ‾ = A + B + C ˉ ‾ + A ˉ + B + C ‾ ‾ ‾ begin{aligned} L & =bar{A} bar{B} C+A bar{B} bar{C}=overline{overline{bar{A} bar{B} C}}+overline{overline{A bar{B} bar{C}}} & =overline{A+B+bar{C}+overline{bar{A}+B+C}} & =overline{overline{overline{A+B+bar{C}}+overline{bar{A}+B+C}}} end{aligned} L=AˉBˉC+ABˉCˉ=AˉBˉC+ABˉCˉ=A+B+Cˉ+Aˉ+B+C=A+B+Cˉ+Aˉ+B+C
参考文献:
- Verilog HDL与FPGA数字系统设计,罗杰,机械工业出版社,2015年04月
- Verilog HDL与CPLD/FPGA项目开发教程(第2版), 聂章龙, 机械工业出版社, 2015年12月
- Verilog HDL数字设计与综合(第2版), Samir Palnitkar著,夏宇闻等译, 电子工业出版社, 2015年08月
- Verilog HDL入门(第3版), J. BHASKER 著 夏宇闻甘伟 译, 北京航空航天大学出版社, 2019年03月





没有回复内容